Organisatie, sterke interactie
 In Evenwicht In Evenwicht
 zijn
die situaties besproken waarin relatief simpele systemen, bestaande uit een
klein aantal op elkaar in werkende onderdelen zoals een gewicht en een veer of
een zon en een planeet, tot een situatie van evenwicht of stabiliteit komen. zijn
die situaties besproken waarin relatief simpele systemen, bestaande uit een
klein aantal op elkaar in werkende onderdelen zoals een gewicht en een veer of
een zon en een planeet, tot een situatie van evenwicht of stabiliteit komen.
In de natuurlijke praktijk gaat het vaak om systemen die uit meerdere elementen
bestaan, die op zich weer evenwichtstoestanden kunnen zijn. Daarin zijn twee
hoofdgroepen te onderscheiden: systemen bestaande uit relatief weinig elementen
met relatief sterke krachten ertussen, en systemen bestaande uit zeer veel
elementen met relatief zwakke krachten ertussen. In dit artikel gaat het om het
eerste geval.
De krachten tussen systemen worden meer algemeen aangeduid als interacties of
"wisselwerking", waarbij dus voor de sterke(re) interacties geldt dat ze meestal
tussen een beperkt aantal elementen gaan. Met als basale geval dat van één-op-één,
bestaande dus uit twee elementen - de situaties uit Evenwicht
 zijn
van deze soort. zijn
van deze soort.
Het beschrijven van twee-deeltjes interacties is de natuurkunde erg goed in,
maar tussen meerdere deeltjes tegelijk wordt het een stuk moeilijker. Een dan
veelgebruikt hulpmiddel is om te kijken naar de geografie van de situatie, en de
daardoor eventueel zichtbare patronen. En dat is hetgeen dat we hier gaan doen,
met het oog op toepassingen in de menswetenschappen. De zichtbare patronen zijn
dan namelijk meteen ook
organisatie-patronen.
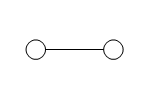 We
starten deze exercitie met een andere regel uit de natuurkunde die we gaan
overnemen in de menswetenschappen: begin met de meest simpele situaties. Dat wil
hier als eerste zeggen: neem alle elementen identiek, en zonder interne
kenmerken - hetgeen je doet door ze voor te stellen als punt, cirkel of
bolletje. Doe iets dergelijks voor de interactie: die stel je voor als lijntje.
Dan wordt de situatie van de één-op-één interactie zoals de figuur hiernaast. We
starten deze exercitie met een andere regel uit de natuurkunde die we gaan
overnemen in de menswetenschappen: begin met de meest simpele situaties. Dat wil
hier als eerste zeggen: neem alle elementen identiek, en zonder interne
kenmerken - hetgeen je doet door ze voor te stellen als punt, cirkel of
bolletje. Doe iets dergelijks voor de interactie: die stel je voor als lijntje.
Dan wordt de situatie van de één-op-één interactie zoals de figuur hiernaast.
 De
volgende stappen zijn voor de hand liggend: breidt het aantal elementen uit tot
drie, vier, enzovoort, zie de figuur hiernaast. Neem aan dat ieder paar
elementen eenzelfde interactie heeft - bij vier elementen zien we wat extra's
gebeuren qua geometrie en patronen: twee "kruis"-interacties. Maar tot zo ver
lijkt er weinig aan de hand. De
volgende stappen zijn voor de hand liggend: breidt het aantal elementen uit tot
drie, vier, enzovoort, zie de figuur hiernaast. Neem aan dat ieder paar
elementen eenzelfde interactie heeft - bij vier elementen zien we wat extra's
gebeuren qua geometrie en patronen: twee "kruis"-interacties. Maar tot zo ver
lijkt er weinig aan de hand.
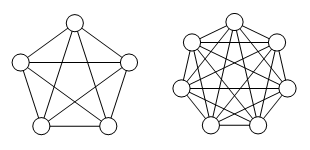 Maar
ga nu verder naar vijf elementen, en meteen maar, om het patroon duidelijk te
maken, naar zeven, zie hiernaast. Wat je dan ziet, is dat het aantal
kruisinteracties razendsnel aan het toenemen is, en de figuur dreigt te gaan
overheersen. Er is weinig verbeelding voor nodig wat er gaat gebeuren bij tien
of meer elementen: er ontstaat één grote grijze massa van verbindingslijnen. Om
voor de hand liggende redenen heet dit patroon het volledig-netwerkmodel (in het
Engels: full mesh). Maar
ga nu verder naar vijf elementen, en meteen maar, om het patroon duidelijk te
maken, naar zeven, zie hiernaast. Wat je dan ziet, is dat het aantal
kruisinteracties razendsnel aan het toenemen is, en de figuur dreigt te gaan
overheersen. Er is weinig verbeelding voor nodig wat er gaat gebeuren bij tien
of meer elementen: er ontstaat één grote grijze massa van verbindingslijnen. Om
voor de hand liggende redenen heet dit patroon het volledig-netwerkmodel (in het
Engels: full mesh).
Nu maken we even een uitstapje naar de praktijk. Stel je voor dat de elementen
mensen zijn, en de interactie een gesprek is. Met vijf deelnemers zou je al
moeite hebben jezelf met iedereen te verstaan, en met zeven is dat al redelijk
ondoenlijk. Het is duidelijk dat veel grotere aantallen niet haalbaar zijn.
Maar stel nu ook eens dat je om een of andere reden toch gedwongen bent om iets
met grotere aantallen mensen te ondernemen. Wat je dan doet, op volkomen
natuurlijk wijze, is de groep opsplitsen. De methodiek van het opsplitsen noemen
we "organisatie". De patronen die je maakt voor het opsplitsen van grotere
groepen zijn organisatiepatronen.
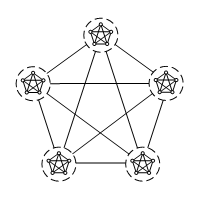 Nu
terug naar de theorie. Stel dat we 25 mensen met elkaar moeten laten
communiceren op een manier die niet tot kakofonie leidt. Dan kijk je naar de
patronen die we al hebben, en zien dat als je opsplitst in vijftallen, je ook
niet te veel groepen krijgt - vijf om precies te zijn. Die groepen kan je dan
ook weer onderling laten communiceren op dezelfde manier als binnen de groepen.
En dus krijg je de nevenstaande figuur een gelaagd-volledig-netwerkmodel. Hierin
zijn er heel veel minder interacties dan bij een echt volledig netwerk, als in
de voorgaande gevallen. Het model heeft twee nadelen: voor interacties tussen
leden van verschillende subgroepen zijn er tussenstappen nodig - en het model
specificeert niet duidelijk hoe die tussenstappen verlopen. Nu
terug naar de theorie. Stel dat we 25 mensen met elkaar moeten laten
communiceren op een manier die niet tot kakofonie leidt. Dan kijk je naar de
patronen die we al hebben, en zien dat als je opsplitst in vijftallen, je ook
niet te veel groepen krijgt - vijf om precies te zijn. Die groepen kan je dan
ook weer onderling laten communiceren op dezelfde manier als binnen de groepen.
En dus krijg je de nevenstaande figuur een gelaagd-volledig-netwerkmodel. Hierin
zijn er heel veel minder interacties dan bij een echt volledig netwerk, als in
de voorgaande gevallen. Het model heeft twee nadelen: voor interacties tussen
leden van verschillende subgroepen zijn er tussenstappen nodig - en het model
specificeert niet duidelijk hoe die tussenstappen verlopen.
 Dit
is dus een oplossing van het hoofdprobleem, maar eentje die toch duidelijk ook
zijn beperkingen heeft. Want voor vijftig mensen heb je al zeven groepen van
zeven nodig, en dat was al weer bijna niet haalbaar. Toch zie je deze oplossing
met enige regelmaat, namelijk als de te onderhouden interactie niet al te intens
of al te ernstig is - zoals bijvoorbeeld bij een groot diner, zie hiernaast. Dan
is ook het aantal tafels goed uitbreidbaar, zoals in de illustratie, omdat de
interacties tussen de tafels nog veel minder in aantal is en veel zwakker
zijn dan binnen één tafel. Dit
is dus een oplossing van het hoofdprobleem, maar eentje die toch duidelijk ook
zijn beperkingen heeft. Want voor vijftig mensen heb je al zeven groepen van
zeven nodig, en dat was al weer bijna niet haalbaar. Toch zie je deze oplossing
met enige regelmaat, namelijk als de te onderhouden interactie niet al te intens
of al te ernstig is - zoals bijvoorbeeld bij een groot diner, zie hiernaast. Dan
is ook het aantal tafels goed uitbreidbaar, zoals in de illustratie, omdat de
interacties tussen de tafels nog veel minder in aantal is en veel zwakker
zijn dan binnen één tafel.
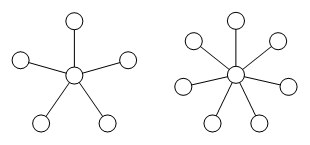 Voor
sterkere interacties, zeg intensieve dialogen en serieuze onderwerpen, zijn de
beperkingen van het gelaagde volledig-netwerkmodel te groot. De menselijke
praktijk geeft hier een oplossing die de natuur ook vaak kiest: het stermodel.
De illustratie van de basale vormen ervan,zie hiernaast, laat meteen de extra
"lucht" zien die dit geeft, doordat een aantal interacties wegvallen. Maar het
model heeft dus ook een nadeel: de interactie tussen twee deelelementen die niet
in het midden staan moet ook in deze basale fase al altijd via een tussenstap,
via het centrumelement, verlopen. Voor
sterkere interacties, zeg intensieve dialogen en serieuze onderwerpen, zijn de
beperkingen van het gelaagde volledig-netwerkmodel te groot. De menselijke
praktijk geeft hier een oplossing die de natuur ook vaak kiest: het stermodel.
De illustratie van de basale vormen ervan,zie hiernaast, laat meteen de extra
"lucht" zien die dit geeft, doordat een aantal interacties wegvallen. Maar het
model heeft dus ook een nadeel: de interactie tussen twee deelelementen die niet
in het midden staan moet ook in deze basale fase al altijd via een tussenstap,
via het centrumelement, verlopen.
 Desondanks
hebben zowel de natuur als de mens de voordelen van het ster-model ingezien. De
natuur plaatst daarbij meestal een speciaal element in het midden, om een
tegenwicht te bieden aan het grote aantal niet-centrale elementen. Zo is het
centrumelement van zowel atoom als planetenstelsel een veel zwaardere "kern",
zie rechts. Desondanks
hebben zowel de natuur als de mens de voordelen van het ster-model ingezien. De
natuur plaatst daarbij meestal een speciaal element in het midden, om een
tegenwicht te bieden aan het grote aantal niet-centrale elementen. Zo is het
centrumelement van zowel atoom als planetenstelsel een veel zwaardere "kern",
zie rechts.
 Bij
de mens wordt de "kern" extra zwaar gemaakt in de rol van de "voorzitter", die
extra rechten krijgt ten opzichte van de overige deelnemers, zoals het recht om
de andere in hun spreekvrijheid te beperken. Maar zelfs in de geometrie, in het
"patroon", is de plaats van de voorzitter vaak herkenbaar, zie de illustratie
links. Bij
de mens wordt de "kern" extra zwaar gemaakt in de rol van de "voorzitter", die
extra rechten krijgt ten opzichte van de overige deelnemers, zoals het recht om
de andere in hun spreekvrijheid te beperken. Maar zelfs in de geometrie, in het
"patroon", is de plaats van de voorzitter vaak herkenbaar, zie de illustratie
links.
 Net
als in het volledig-netwerk geval kan ook het stermodel uitgebreid worden naar
grotere groepen, door subgroepen te creëren. Dan krijg je de situatie van
hiernaast, voor het geval van een zeven-bij-zeven sternetwerk. Vergelijking met
het vijf-bij-vijf volledig-netwerk laat zien dat het sternetwerk bij het dubbele
aantal elementen toch overzichtelijker is, en bovendien biedt het sternetwerk
een natuurlijke manier van interactie tussen de subgroepen: die kan plaatsvinden
tussen de centrum-elementen van die groepen. Waarmee men dus een nieuwe laag in
de hiërarchie krijgt: het centrumelement van de centrumelementen. Net
als in het volledig-netwerk geval kan ook het stermodel uitgebreid worden naar
grotere groepen, door subgroepen te creëren. Dan krijg je de situatie van
hiernaast, voor het geval van een zeven-bij-zeven sternetwerk. Vergelijking met
het vijf-bij-vijf volledig-netwerk laat zien dat het sternetwerk bij het dubbele
aantal elementen toch overzichtelijker is, en bovendien biedt het sternetwerk
een natuurlijke manier van interactie tussen de subgroepen: die kan plaatsvinden
tussen de centrum-elementen van die groepen. Waarmee men dus een nieuwe laag in
de hiërarchie krijgt: het centrumelement van de centrumelementen.
Het gelaagde sternetwerk is daarom een veelvoorkomende manier om grotere
hoeveelheden elementen te organiseren - de natuur doet het bijvoorbeeld in
sneeuwvlokken en bloemen, zie de illustraties onder:
De illustraties (rechts een Agapanthus orientalis) laten ook zien dat de natuur
niet de precieze vormen van onze schema's volgen, maar wel in redelijke
benadering. De mens gebruikt sternetwerken bijvoorbeeld in de techniek: de
communicatienetwerken van telefonie en internet zijn grotendeels gelaagde
sternetwerken.
De laatste hier besproken soort netwerk is ook veelvoorkomend, zoals de naam al
laat zien: het boom-netwerk. Daarvan geven we meteen de basale vormen in één
figuur:
De eerste figuur lijkt wat raar: een boom met twee takken. Maar dit heeft wel
degelijk een sociologisch analogon: het geval dat twee partijen niet direct met
elkaar kunnen praten, maar alleen via een tussenpersoon - het geval van "mediation".
Het boomnetwerk heeft veel weg van het sternetwerk - het is slechts een kwestie
van wat herschikking van de niet-centrum elementen (veel wiskundigen zouden de
modellen zelfs als identiek beschouwen). Maar ook hier geeft de geometrie van
het patroon extra informatie: in de hier gegeven vorm van de boomstructuur heeft
het centrumelement een bovenliggende plaats - in de werkelijke wereld
overeenkomende met een bovenliggende sociale positie of machtspositie.
Die laatste vorm van analyse kan zelfs nog een stapje verder uitgewerkt worden.
Neem de drie gevallen van een boom met drie, vijf, en een extra grote stap
nemende, negen randelementen, en houd de hoogte van de patronen dezelfde:
Het is duidelijk dat de elementen verder op de rij steeds verder weg liggen en
de lijnen langer worden, en als we gaan praten over de interacties waarvoor de
lijnen staan, die interacties waarschijnlijker zwakker.
Een oplossing om de interacties ongeveer constant te houden, is om de hoogte van
het patroon te vergroten, zie de volgende reeks figuren:
Maar dit heeft dus het gevolg dat de afstand tussen centrum-element en de
niet-centrum-elementen groter wordt.
Dit zijn zaken die je regelrecht kan terugvinden in de ervaringen met menselijke
organisaties. Het eerste patroon illustreert het probleem van "Het verliezen van
contact met een deel van het werkveld". Het tweede patroon vertaald zich als
"Hoe groter de organisatie, hoe verder weg de baas staat". Een volgende bewijs
van de kracht van de methodiek van de geografie van patronen voor menselijke
zaken.
Het boomnetwerk is het enige dat zich hier, blijvende bij onze
standaardvormgeving, leent voor een weergave van meer dan twee niveaus, hoewel
zelfs dan een kleine kunstgreep noodzakelijk is door wat subgroepen te op te
rekken:
Een essentieel element in deze beschrijving is het punt waarop het stijgende
aantal elementen de introductie van nieuwe subniveaus wenselijk of noodzakelijk
maakt - want dit bepaalt dus in hoge mate de vorm van het uiteindelijke
eindresultaat.
Een eerste aanwijzing voor de plaats van die grens vindt men in de
computerwereld. De structuur van folders in een computer is een zuivere
boomstructuur - knooppunten zijn de de folders en eindpunten de bestanden. Een
bekende richtlijn om te gaan denken over het maken subfolders in een bestaande
folder, is als het aantal bestanden ergens in de reeks van tien tot twintig
ligt, afhankelijke van de diversiteit - en bij vijftig of honderd weet je dat
zeker.
De menselijk-organisatorische versie van dit proces is te vinden in een
verhaal uit één van de allereerste boeken over organisaties: Parkinson's Law
(1958)
 van C. Northcote Parkinson. Dit boek is geschreven als satire, maar het is zeer
geslaagdals satire omdat het gebaseerd is op voor iedereen zeer bekend
voorkomende processen. Het hier relevante hoofdstuk heet Directors and
Councils, ondertitel: Coefficient of Inefficiency. Het beschrijft
onder andere de evolutie van de diverse vormen van de Engelse kabinetten,
beginnende met het Lords of the King's Council (1257), via Privy
Council en Cabinet Council, naar het huidige Cabinet. Het
proces loopt als volgt: bij aanvang van het instituut telt het iets als vijf tot
tien leden. Er komen er steeds meer bij (baantjes te vergeven door de koning,
weet u wel), tot het zaakje onwerkbaar wordt, waarna het echt belangrijke
subgroepje zich afscheidt, enzovoort. In de huidige moderne Westerse kabinetten
van rond de twintig leden heb je ook weer een onofficieel kernkabinet van circa
vijf ministers (minister-president, financiën, economie en/of sociale zaken,
binnenlandse en/of buitenlandse zaken - al naar gelang de te bespreken
kwesties). Ook heel illustratief voor de relatie tussen omvang en effectiviteit
is het lijstje van landen versus omvang van hun kabinetten - tezamen met wat
citaten uit Parkinson's Law te vinden hier
van C. Northcote Parkinson. Dit boek is geschreven als satire, maar het is zeer
geslaagdals satire omdat het gebaseerd is op voor iedereen zeer bekend
voorkomende processen. Het hier relevante hoofdstuk heet Directors and
Councils, ondertitel: Coefficient of Inefficiency. Het beschrijft
onder andere de evolutie van de diverse vormen van de Engelse kabinetten,
beginnende met het Lords of the King's Council (1257), via Privy
Council en Cabinet Council, naar het huidige Cabinet. Het
proces loopt als volgt: bij aanvang van het instituut telt het iets als vijf tot
tien leden. Er komen er steeds meer bij (baantjes te vergeven door de koning,
weet u wel), tot het zaakje onwerkbaar wordt, waarna het echt belangrijke
subgroepje zich afscheidt, enzovoort. In de huidige moderne Westerse kabinetten
van rond de twintig leden heb je ook weer een onofficieel kernkabinet van circa
vijf ministers (minister-president, financiën, economie en/of sociale zaken,
binnenlandse en/of buitenlandse zaken - al naar gelang de te bespreken
kwesties). Ook heel illustratief voor de relatie tussen omvang en effectiviteit
is het lijstje van landen versus omvang van hun kabinetten - tezamen met wat
citaten uit Parkinson's Law te vinden hier
 .
.
Deze toepassingen in de menselijke wereld, net als die uit de rest van de
natuur, laten nogmaals zien dat de werkelijke wereld niet de strikte schema's
zoals hier gehanteerd volgen. De werkelijke patronen zijn niet zo regelmatig, de
diverse subpatronen kunnen van een andere soort zijn, en de grenzen zijn niet
scherp te trekken. Maar dat zijn ook dingen die je kan proberen in de
theoretische schema's kan verwerken.
Dat laatste is al gedaan voor structuren die zich vooral kenmerken door vele
subniveaus. De beschrijving van dat soort structuren vindt men in het kader van
de studie van fractals, fractale structuren, met als meeste simpele
voorbeeld de Lindenmayer-boom
 . Hier laten we zien hoe je een Lindermayer-boom
maakt uit een basaal schema van de soort die we al kennen. . Hier laten we zien hoe je een Lindermayer-boom
maakt uit een basaal schema van de soort die we al kennen.
We gaan uit van een twee bij twee boomnetwerk naar ons eerdere model, onder
links. Waarvan we de cirkeltjes als knooppunten weglaten, en daarna omkeren, zie
onder midden, waarna we nog twee subniveaus toevoegen, onder rechts:
In het oorspronkelijke schema zijn de takken van het eerste niveau wijder uit
elkaar dan van het tweede, om het geheel overzichtelijker te houden - doe je dat
niet, komen de elementen van het twee niveau te dicht bij elkaar te liggen. Dit
herhaalt zich in de volgende niveaus.
 Een
Lindenmayer-boom krijg je door niet de takken naar elkaar toe te brengen, maar
op ieder nieuw niveau de hele
V een beetje naar buiten te draaien - en het
patroon consequent te maken door de onderste V
net als de rest ook te laten ontspringen uit een
I - zie het resultaat rechts, voor het geval
van zeven niveaus. Een
Lindenmayer-boom krijg je door niet de takken naar elkaar toe te brengen, maar
op ieder nieuw niveau de hele
V een beetje naar buiten te draaien - en het
patroon consequent te maken door de onderste V
net als de rest ook te laten ontspringen uit een
I - zie het resultaat rechts, voor het geval
van zeven niveaus.
Maar die figuur is duidelijk nog iets wiskundigs: te symmetrisch, te regelmatig,
en met lijntjes zonder "body". Geef de lijntjes body en breng wat
asymmetrie erin, en maak de hoeken wat groter, en je krijgt de afbeelding onder
links. Nog wat meer willekeur, en kleur en omgeving erbij, en je krijgt het
plaatje onder rechts (let op: ook deze boom is op de beschreven manier door de
computer gegenereerd - ook dit is een Lindenmayer-boom):
Wat deze theoretische exercitie laat zien, is dat datgene dat zich aan ons oog
voordoet als een heleboel willekeur met een beetje regelmaat, best wel het
resultaat kan zijn van een onderliggend proces met behoorlijk veel regelmaat en
daarbij enige willekeur.
Let overigens op dat in tegenstelling tot wat je zou verwachten, je de meest
realistische resultaten bereikt door te beginnen met een zeer simpel geval: een
twee-bij-twee netwerk. Dit is ook een zeer sterke regel in de natuur:
ingewikkelde zaken worden opgebouwd uit simpele. De levende natuur doet dat
voornamelijk door twee processen: reproductie en aantrekking. Die dan ook in het
Lindenmayer model zijn ingebouwd, zoals verder wordt uitgelegd hier
 .
.
 Waar
we het tot nu toe voornamelijk gehad hebben over de geometrie van de patronen,
laat het voorbeeld van de Lindenmayer-boom ook zien dat de rol van de
aantrekking, dat wil zeggen: de interactie, cruciaal is. Een redelijk sterke
regel daarbij is: hoe sterker de interactie, hoe duidelijker de regelmaat - zie
de nevenstaande illustratie van sneeuwkristallen, die ieder voor zich even
individueel zijn als een individueel mens ten opzichte van zíjn groep, maar
waarvan bij de sneeuwkristallen de achterliggende sterke regelmaat even volkomen
duidelijk is Waar
we het tot nu toe voornamelijk gehad hebben over de geometrie van de patronen,
laat het voorbeeld van de Lindenmayer-boom ook zien dat de rol van de
aantrekking, dat wil zeggen: de interactie, cruciaal is. Een redelijk sterke
regel daarbij is: hoe sterker de interactie, hoe duidelijker de regelmaat - zie
de nevenstaande illustratie van sneeuwkristallen, die ieder voor zich even
individueel zijn als een individueel mens ten opzichte van zíjn groep, maar
waarvan bij de sneeuwkristallen de achterliggende sterke regelmaat even volkomen
duidelijk is
 . Hetgeen wordt veroorzaakt door de relatief sterke interactie tussen de
watermoleculen die het sneeuwkristal vormen, en alles in een zesvoudige
symmetrie duwen.
. Hetgeen wordt veroorzaakt door de relatief sterke interactie tussen de
watermoleculen die het sneeuwkristal vormen, en alles in een zesvoudige
symmetrie duwen.
In de levende natuur zijn de interacties voornamelijk van de zwakkere soort, en
dat zie je dus in het niet-scherp (symmetrisch) zijn van de patronen, zie de
Agapanthus-bloem boven, en het mengen van diverse organisatiepatronen. Maar dat
doet er dus kennelijk allemaal niet aan af dat uit de bestaande achterliggende
regelmaat in de patronen wel degelijk conclusies getrokken en voorspellingen
gehaald kunnen worden, omtrent dat soort inschattingen als wat wel werkbaar is,
en wat niet. Zoals de intuïtie doet al doet, ongetwijfeld door die patronen te
herkennen en mee rekening te houden.
Wat betreft menselijke toepassing hebben we al een paar voorbeelden gezien, in
de vorm van het gebeuren van overleg en vergadering. Daarbij ging het ook
voornamelijk over het patroon en de geometrie (tijdens international vergadering
speelt de vorm van de tafel waaraan men zit ook een dusdanig cruciale rol, dat
hiervoor een speciale term is: een "ronde-tafel-conferentie").
Maar ook bij menselijk gedrag speelt de aard van de interactie een belangrijke
rol. En ook hier blijkt de regel van simpelheid opgeld te doen: wil je gedrag
besturen, dan blijkt in eerste instantie de meest simpele regel het beste te
voldoen: tit-for-tat
 .
.
Een andere menselijke toepassing van de aard van de interactie gaat over een
heel apart geval: dat van de afstoting. Nu is afstoting op zichzelf, als enige
interactie, geen interessant geval, want dat betekent dat de losse elementen
steeds verder van elkaar af bewegen, en je gewoon een grote uitdijende wolk
zonder enkele structuur krijgt.
Een interessante afstoting is dus altijd een secundair verschijnsel ten opzichte
van een al bestaande aantrekking. In het menselijke geval hebben we het voor de
afstoting dan over zaken als afkeer van vreemden en aanverwante, als extra
binnen een maatschappij met bestaande bindingen. Dat is dus slechts een
uitbreiding van het bestaande model en ook het geval van afstoting valt dan ook
met patronen en modellen te beschrijven - meer daarover hier
 .
.
Tot zover de eerste versie van de behandeling van de sterke interactie - latere
wijzigingen en uitbreidingen zijn, gezien de reikwijdte van het proces,
waarschijnlijk - een directe toepassing in de sociologie begint hier
 .
Methodologisch gaat het verder met de tweede belangrijke hoofdvorm van
organisatie: de
zwakke interactie .
Methodologisch gaat het verder met de tweede belangrijke hoofdvorm van
organisatie: de
zwakke interactie
 . .
Naar Menswetenschappen, regels
 , of site home
, of site home
 ·. ·.
|